awaregasil.blogg.se - Which piecewise relation defines a function

#WHICH PIECEWISE RELATION DEFINES A FUNCTION HOW TO#
#WHICH PIECEWISE RELATION DEFINES A FUNCTION SERIES#

An explicit definition of the sequence might even use a formula, say \(x_n = 2n+5\text\) A sequence \(x\) defined a map \(n \mapsto x_n\) from the value of the index to the value in the sequence list at that index position. We earlier learned that sequences are functions. A function is a mapping from a set of inputs (the domain) to a set of possible outputs (the codomain ). Continuity requires that the function is defined and that the left- and right-limits both agree with the actual function value. We learn about limit notation as a way of evaluating what a rule to the left or right of a point would have given at a point. With piecewise functions, a function might not be continuous. Other times, we need the function to use different rules on different sets, creating a piecewise function. Sometimes, we need to restrict a function to use a rule only on a particular set, called the explicit domain. A function is one that has a unique value of the dependent variable for each value of the independent variable in. Finding the natural domain of a function involves solving inequalities using sign analysis. Recall that all relations are not functions.

#WHICH PIECEWISE RELATION DEFINES A FUNCTION HOW TO#

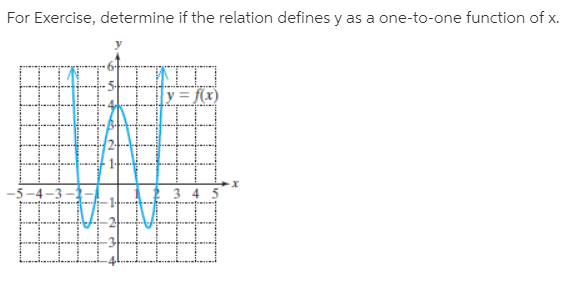
We learn about the domain of the function and how to find the domain given a formula. In this section, we consider how functions are defined on different sets. Section 5.2 Functions Defined on Intervals ¶ Overview. Recursive Sequences and Projection Functions.Each definition uses Set-Builder Notation: notation The first definition views the. Integrals and the Method of Substitution worksheet piecewise functions answer key.Only the 3rd Image matches 1 x-value to every 1 y-value. In Images 1, 2, and 4, there are certain inputs that have two outputs or stated otherwise, have two y-values for the same x-value. Derivatives of Inverse Trigonometric Functions The 3rd Image defines a piecewise function because for it to be a function, every input must match to exactly one and only one output.The Derivatives of Trigonometric Functions.Implicit Differentiation and Derivatives of Inverse Functions.The Derivative of Exponential Functions.

Calculating Integrals Using Accumulations.

Accumulation Functions and the Definite Integral.

The Fundamental Theorem of Calculus, Part One.

The function is the constant function V ( t) 0, when t < 0, but a different constant function, V ( t) 5, when t 0. Here are real-life examples of relations and functions. Because each of the pieces in this definition is constant, the function V is called a piecewise constant function.

#WHICH PIECEWISE RELATION DEFINES A FUNCTION SERIES#

Rate of Accumulation and the Derivative A piecewise function is a function defined by a series of intervals for the independent variable.